Multivariate Linear Regression Analysis - Blog | Full Stack Web Developer, Artificial Intelligence Specialist

Multivariate Linear Regression Analysis

Predict lending interest rate using multivariate linear regression analysis

Data example

credit_card

0.1071

228.22

11.08214255

14.29

707

debt_consolidation

0.1357

366.86

10.37349118

11.63

682

debt_consolidation

0.1008

162.34

11.35040654

8.1

712

credit_card

0.1426

102.92

11.29973224

14.97

667

credit_card

0.0788

125.13

11.90496755

16.98

727

debt_consolidation

0.1496

194.02

10.71441777

667

all_other

0.1114

131.22

11.00209984

11.08

722

home_improvement

0.1134

87.19

11.40756495

17.25

682

debt_consolidation

0.1221

84.12

10.20359214

707

debt_consolidation

0.1347

360.43

10.4341158

22.09

677

debt_consolidation

0.1324

253.58

11.83500896

9.16

662

debt_consolidation

0.0859

316.11

10.93310697

15.49

767

small_business

0.0714

92.82

11.51292546

6.5

747

debt_consolidation

0.0863

209.54

9.487972109

9.73

727

major_purchase

0.1103

327.53

10.73891524

13.04

702

all_other

0.1317

77.69

10.52277288

2.26

672

credit_card

0.0894

476.58

11.60823564

7.07

797

debt_consolidation

0.1039

584.12

10.49127422

3.8

712

major_purchase

0.1513

173.65

11.00209984

2.74

667

all_other

0.08

188.02

11.22524339

16.08

772

CSV file with full data can be accessed here:
https://nick.fit//blog/linear-regression-analysis/loan_data.csv

Let's say you have a task where you have to predict lending interest rate charged to the borrower having the data above. First, import data:

import pandas as pd
import numpy as np
import statsmodels.api as sm
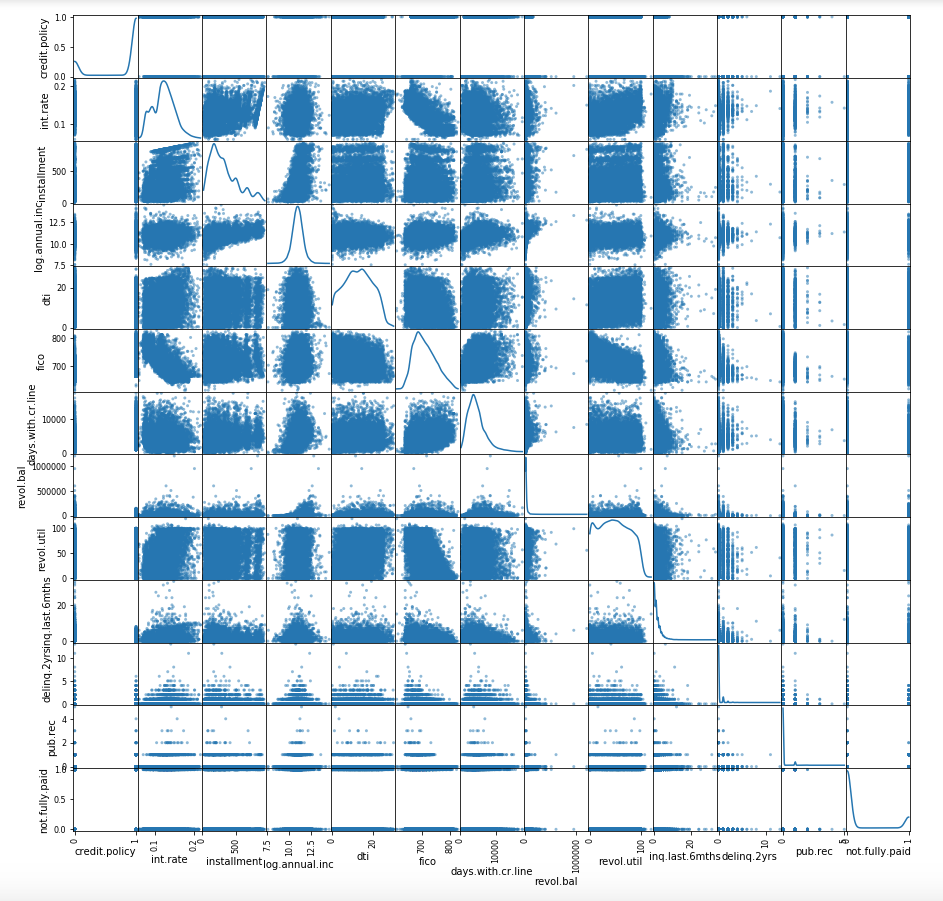
loansData = pd.read_csv('loan_data.csv')

In order to be able to understand which fields from the CSV file affects seeking interest rate we have to build Scatterplot Matrix first. For reference https://en.wikipedia.org/wiki/Scatter_plot

pd.plotting.scatter_matrix(loansData,figsize=(15,15),diagonal='kde')

If you pay attention "int.rate" does not depend on ["credit.policy", "revol.bal", "inq.last.6mths", "delinq.2yrs", "pub.rec", "not.fully.paid"]. It doesn't depend because for each different "int.rate" value corresponds almost the same value from mentioned columns. Thus we can skip these columns. For the rest columns we are going to create linear model using OLS from statsmodels

interestRate = loansData['int.rate']
installment = loansData['installment']
logAnnualInc = loansData['log.annual.inc']
dti = loansData['dti']
fico = loansData['fico']
daysWithCrLine = loansData['days.with.cr.line']
revolUtil = loansData['revol.util']

y = np.matrix(interestRate).transpose()
x1 = np.matrix(installment).transpose()
x2 = np.matrix(logAnnualInc).transpose()
x3 = np.matrix(dti).transpose()
x4 = np.matrix(fico).transpose()
x5 = np.matrix(daysWithCrLine).transpose()
x6 = np.matrix(revolUtil).transpose()

x = np.column_stack([x1,x2,x3,x4,x5,x6])
# create a linear model
X = sm.add_constant(x)
model = sm.OLS(y,X)
f = model.fit()

print ("pvalues = %s, rsquared = %s" % (f.pvalues, f.rsquared))
print ("Intercept = %s, Coefficients = %s" % (f.params[2], f.params[0:2]))

P-Values are probabilities. The convention is it needs to be 0.05 or less:
https://en.wikipedia.org/wiki/P-value
R-squared is a measure of how much of the variance in the data is captured by the model. A high R-squared would be close to 1.0 a low one would be close to 0. The value we've got = 0.63, is a good one.
https://en.wikipedia.org/wiki/Coefficient_of_determination
Trying to decrease number of depended variables (currently we've got 6) and keeping eye on P-Values and R-squared we end up with x1 and x4 will produce almost the same values be had before.

x = np.column_stack([x1,x4])

Formula

where a0 is the Interceptor and a1, a2 are Coefficients for Installment and Fico respectively. Thank you for reading to the end :)

Technologies

Python
statsmodels
Scatterplot Matrix